GeoGebra and Sage

Looks like there is some momentum building to integrate GeoGebra applets into the Sage notebook, which I think would be fantastic. I've been lazy about checking out GeoGebra until now, despite hearing good things about it. Dan Drake's demonstration of a nice applet made in less than an hour of experimenting inspired me to give it a try. In ten minutes I had downloaded GeoGebra, installed it, made a simple demo and moved it to my university account. I am very impressed, and hope to help a little to get this into Sage.

Plucker's Quartic Curve

A quartic curve in the plane has a maximum of 28 real bitangents. Plucker came up with the following sort of example that attains that bound, which I illustrated in a particular case with phcpack and Sage:

More polytopal animations

I was inspired by a still image from the Wikipedia entry on the 24-cell to make an animation of rotating and then stereographically projecting the 24-cell, showing the images of the original polytope edges. Math on Wikipedia is pretty spotty, but the polytope entries have really become top-notch in the last few years.
Here's a still from the animation:



and a medium and small resolution version of the animation:

small (300x300, 6 MB)
medium (512x512, 17 MB).

600-cell animations

Over the last year or so, when I have time, I've been trying to fine tune ray-traced animations of polytopes (using Sage, Tachyon, ffmpeg, and cddlib). My latest effort was to do a loop of Schlegel projections of the beautiful 600-cell. The 600-cell is one of the six regular polytopes in 4 dimensions; its usually considered the 4D analog of the icosahedron. Here's a still from my animation:



Since Blogger's re-encoding butchers my movies, I will just post links. Here are four sizes:

small (320x200, 3.5 MB)
medium (640x400, 7 MB)
large (1280x800, 13 MB)
large, high-res (1280x800, 33 MB).

Twenty Four Cell, take 2

Hmm...blogger re-encodes my video and for some reason their version looks like crap, so I won't even leave it up. I think my new attempt has much better lighting, and the faces have translucent panes now. But here is a still shot:



Three sizes of the new version:
small (320x200)
medium (640x400)
large (1280x800).

Witch of Maria Agnesi

There's one on wikipedia like this, but for an upcoming class I wanted to do it in Sage:




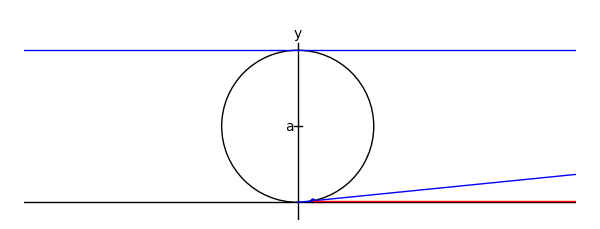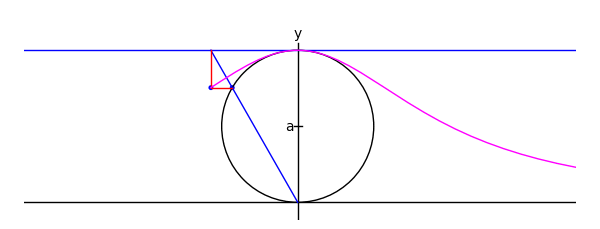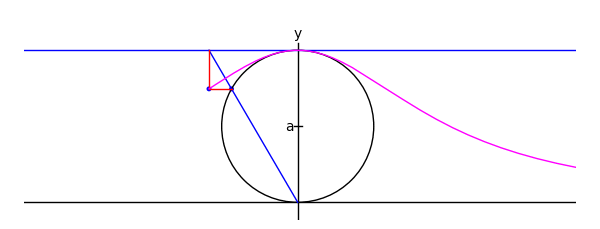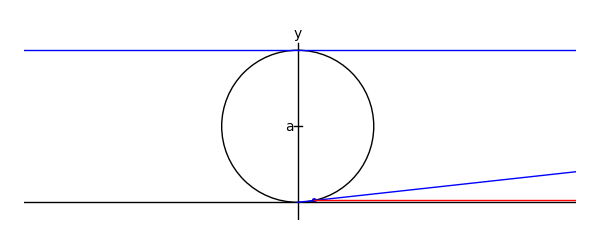
xtreme = 4.1
myaxes = line([[-xtreme,0],[xtreme,0]],rgbcolor = (0,0,0))
myaxes = myaxes + line([[0,-1],[0,2.1]],rgbcolor = (0,0,0))
a = 1.0
t = var('t')
npi = RDF(pi)
def agnesi(theta):
mac = circle((0,a),a,rgbcolor = (0,0,0))
maL = line([[-xtreme,2*a],[xtreme,2*a]])
maL2 = line([[0,0],[2*a*cot(theta),2*a]])
p1 = [2*a*cot(theta),2*a*sin(theta)^2]
p2 = [2*a*cot(theta)-cot(theta)*(2*a-2*a*sin(theta)^2),2*a*sin(theta)^2]
maL3 = line([p2,p1,[2*a*cot(theta),2*a]], rgbcolor = (1,0,0))
map1 = point(p1)
map2 = point(p2)
am = line([[-.05,a],[.05,a]], rgbcolor = (0,0,0))
at = text('a',[-.1,a], rgbcolor = (0,0,0))
yt = text('y',[0,2.2], rgbcolor = (0,0,0))
xt = text('x',[xtreme + .1,-.1], rgbcolor = (0,0,0))
#tt = text('t',[.15,.1], rgbcolor = (0,0,0))
matext = at+yt+xt
ma = mac+myaxes+maL+am+matext+maL2+map1+maL3+map2
return ma

def witchy(theta):
ma = agnesi(theta)
agplot = parametric_plot([2*a*cot(t),2*a*sin(t)^2],[t,.001,theta], rgbcolor = (1,0,1))
return ma+agplot

a2 = animate([witchy(i) for i in srange(.1,npi-.1,npi/60)]+[witchy(i) for i in srange(npi-.1,.1,-npi/60)], xmin = -3, xmax = 3, ymin = 0, ymax = 2.3, figsize = [6,2.3], axes = False)

a2.show()


24 cell movie

This is basically a test of my workflow for a more ambitious project, but its somewhat amusing in its own right. The original 48 MB version is here (much better quality).

Michael Corral's Calculus 3 book

Last year I became aware of the fantastic free calc 3 book by Michael Corral. His website for it is here. I wanted to be able to compile the latex source files myself but couldn't get it to work on my mac or windows machines. I just gave it another try and finally succeeded on OS X.

Besides using his calc3book.sh script, I found it necessary to:

1) install pgf/tigz.
2) put picins.sty in my tex directory
3) Put the metapost files from m3Dplain in my tex directory.

Its a beautifully done book, so I am excited to learn some of the tricks Corral uses.

Hearing a trigonometric identity

If you force a harmonic oscillator with natural frequency w_0 with a sinusoidal force of frequency w, the resulting steady-state is a linear combination of those two frequencies. If its something in the audible range, you hear either the two seperate frequencies or one frequency with a beat if they are close together. In other words, you hear either the right or left hand side of the identity shown below.



Sage source code available here. Ironically, because of my use of html I can't seem to show the source directly here.

Small frequency difference.

Smallish frequency difference (close to the Ma Bell tone).

Intermediate frequency difference.

Large frequency difference - you definitely hear it as a 2-note chord.

symmetry in chaos

Recently SIAM had a deal to get some books from their catalog cheap if you bought the new edition of "Symmetry in Chaos" by Field and Golubitsky. So I did, and couldn't help but try to reproduce some of their figures. I think they might have a typo in their parameters for their figure 2.3 (or I am making some mistake, quite likely), but after exploring a bit with other parameters I got the following, with iterates of

Mixmead

Recipe:

1.5 lbs Late Summer Wildflower Honey (Talking Oak Farm, WI)
3 lbs Northern Brewer Orange Blossom Honey (CA)
3 lbs Skalko's Honey Bee Farm Honey
3 lbs Duluth Whole Foods Coop (not the chain) Honey
1 cup Northern Brewer Gold Malt Extract
1 handful o' hops from Grant Anderson
Lalvin EC-1118 S.bayanus Champagne Yeast
...after 2 months added 1/2 cup of Adro Hungarian Forest Honey (great stuff)
...after 7 months added 1/4 cup of brown sugar and 2 Ceylon teabags
...bottled after 9 months with another 2 bags of Chai Black Tea.

All the tea is to offset the sweet taste - the champagne yeast should have gobbled it up but at the 7 month point it was still too cloying for me. Now it tastes pretty good...

Two recipes: beer and biscotti

I tried two experiments this weekend, a beer and a variation on a biscotti recipe.

I won't know how good the beer is for another 2 months or so. Here is the ingredient list:

Wayward Monk Ale

• 6 lbs Northern Brewer Amber Malt Extract


• 3.15 lbs Northern Brewer Dark Malt Extract


• 1 1b Dark Belgian Candi Sugar


• Wyeast Belgian Abbey II yeast (#1762)


• 1 oz Fuggle hops


• 1 oz Saaz hops


• 1 oz Hallertau Mittelfruh hops


• 1 gm of Myrica gale


• 1 pinch of Wormwood


• 1 lbs Belgian Biscuit Malt


• 1 lbs Franco-Belges Kiln Coffee Malt

The last two ingredients I forgot to order, and they will have to be added later. I'm not sure what effect that will have. I'm also not sure what this beer will be like - its kind of a winter-warmer/scotch ale/Belgian abbey hybrid. But that's why I homebrew - why make something you can buy in a store?

The biscotti is already a clear success. The recipe is essentially from Baking Illustrated, which I highly recommend.

• 2 cups of flour (I like to use some whole wheat in there)


• 1 tsp baking powder


• 1/2 tsp salt


• 3 tbsp unsalted butter


• 1 cup sugar (I like to use some portion of brown sugar)


• 2 eggs


• 1/2 tsp vanilla extract


• 2 oz sliced almonds, roasted briefly in a pan


• 1/2 cup of cocoa nibs (I used the organic Dagoba ones, which are the only thing I have ever seen in a supermarket)

You make the dough into two loaves, cook for about 25 minutes at 350 F. Take it out and slice into strips, then rebake at 325 for about 15 minutes. Its very easy but seems to impress people as much as much more difficult baked goods.

Polytopes in Sage, take 1

Here's a first attempt at a short video intro to polytopes in Sage. Sage 4.0, which should be released soon, has some new functionality that was added during Sage Days 15 (thanks to David Perkinson for reviewing some of that, and Rob Beezer for helping David learn the review ropes).

The video is about 4 MB and can be found here. I am not sure how the format will work on other computers so if anyone takes a look and it doesn't work let me know. Also, I am interested in getting constructive criticism on the video.

boolean Adelaide

Just a little follow-up post to my Adelaide Venn diagram post. I wanted to double-check its correctness, so I made this diagram showing whether each set was included or not. Color by numbers!

Protein of the Day #20: Sirtuin1

This week there is an set of articles in Science on the protein Sirtuin1. The sirtuin family is very interesting, involved in ageing, epigenetic gene silencing, and other cellular regulation. The Science articles provide some new links of Sirtuin1 to circadian rhythms and matebolism.

Here's a static shot of the common 3D domain of the sirtuin superfamily:



The NAD+ dependence of Sirtuin1 seems to be an important link between the circadian system, the metabolic state of the cell, and genetic regulation. As always, I am wondering if there are connections here to mammalian hibernation...

Slouching towards Adelaide

At some point when I was in grad school I became aware of some work on symmetric Venn diagrams. If you google this, you will find this link, which has been maintained but not changed too much since 1997. Other than that, there isn't a lot on the web and there is a particular lack of quantitative direction on how to construct the beautiful rotationally symmetric Venn diagrams such as Adelaide. This was named by Anthony Edwards after the city in which he discovered it. I have always wanted to go to Adelaide, it holds a strange attraction for me, so perhaps that is why that particular 7-set Venn diagram stuck in my head.

When I started working on my coloring book, I immediately thought of the Adelaide diagram but I didn't know how to construct it. After some mistakes today, I think I finally have it down. Here is a colored version:



Code (in Sage) for some version of this will be in the final coloring book.

Mixmead

I've had a mead going for quite a while now - started on September 6th, 2008 - which I just racked for a second time. Its proving to be a troublesome brew, perhaps because I never had a clear vision of what it was supposed to be. I have been calling it the "Mixmead" since its a hodgepodge of all sorts of honey that I was able to get in 2008. Here's the exact recipe:

1. 1.5 lbs Late Summer Wildflower Honey (Talking Oak Farm, WI)


2. 3 lbs Northern Brewer Orange Blossom Honey (CA)


3. 3 lbs Skalko's Honey Bee Farm Honey (Esko, MN)


4. 3 lbs Duluth Whole Foods Coops Honey (God Knows Where, USA)


5. 1 cup Northern Brewer's Gold Malt Extract (for protein, rather than that nasty chemical mead nutrient)


6. 1 handful o'hops from Grant Anderson (thank you Grant!)


7. Lalvin EC-1118 Sabayanus Champagne yeast (Champagne yeast:beer yeast::SWAT team:suburban cop)

I racked this on November 16th, 2008, and added 1/2 cup of Hungarian Adro Forest Honey (fantastic stuff). Tasted too sweet then, despite the commando-like efforts of the champagne yeast.


This second racking, I added a tiny bit (3/16 cup) of brown sugar and 2 heavily steeped tea bags of some rather bitter Ceylon tea. I hope the tea will cut the excessive sweetness a bit (this is a pretty traditional thing to add to meads).


If all goes well, this will be bottled in a month.

Cayley Cubic

To further my polynomial education I've been thinking some lately about the Cayley cubic, which in the affine form I was using is given by x^2 + y^2 + z^2 + z(y^2-x^2) -1 = 0.

I made a little movie of some of the real solution set of the Cayley cubic. Here's one of the stills:

I think the quicktime version works better in browsers, or you can download a slightly higher-quality mp4.

Protein of the Day #19: Fto (Fatso)

Protein names are funny things. Often they are chosen before much of the functionality of the protein is characterized, which means they are usually misleading. I wonder how much progress in biology has been retarded over the years by that simple fact.

The abbreviation Fto comes from "fused toes" mutation, but was also initially called Fatso because it is a relatively large protein (about 500 amino acids, nothing close to the huge ones like titin). Ironically, this name is quite important since it seems that Fto is very important in energy homeostasis in mammals. It is highly expressed in the arcuate nucleus. There is some correlation between Fto mutations and susceptibility to diabetes. Because of all that, the preferred descriptive name now is "fat mass- and obesity-associated gene".

Protein of the Day #18: Cruciferina

Cruciferina: sounds like an all-girl punk group or something. I couldn't find out too much about it, its a cupin-superfamily protein that is a desiccation-tolerant seed storage globulin. "Cupin" comes from the Latin "cupa" for small barrel; cupin proteins have a beta-barrel motif that apparently is useful for all sorts of things. Here's one representation of the barrel (not from Cruciferina in particular) from topsan.org:



Various cupin proteins seem to heavily expressed in the floral nectary tissues studied in my friend Clay Carter's lab.

Books I am reading right now

Fiction:

0a. Anathem, by Neal Stephenson. I finished this one, but I am including it because I liked it so much. Not that Neal needs much advertising.

0b. The Algebraist, by Iain Banks. Fantastic cover, at least the US paperback. I finished this while in South Africa too, but it was one of my favorites this year.

1. The Sacred Book of the Werewolf, by Victor Pelevin. Trippy, odd, hard to describe - but good.

2. Wizard of the Crow, by Ngugi Wa'Thiong'O. Sort of like 100 Years of Solitude in Africa.

3. Victory of Eagles, by Naomi Novik. Good series.

4. Turn Coat, by Jim Butcher. I think I have read everything by him, he doesn't disappoint.

Non-fiction (I am leaving out a lot of math and bio books):

1. Imagining India, by Nandan M. Nilekani. Very good book about modern India, where its going and how it got there.

2. The Manga Guide To Statistics, by Shin Takahashi. Surprisingly good. The Manga Guide to Databases is also pretty good.

Curves of Pursuit

When I visited Stellenbosch University in February, I noticed the math department had some nice posters on various mathematical topics that I thought could be implemented in Sage. The only one I did was "Curves of Pursuit", in which one has n points in a regular n-gon, and each point chases the next. The solutions are prettier when discrete time steps are taken. You can see the code at

http://wiki.sagemath.org/interact/graphics#CurvesofPursuit

Protein of the Day #17: mTOR

mTOR (mammalian target of rapamycin) does a whole lot of things, as the attempted pathway image below shows (from Wikipedia, which I am not ashamed to link to for biochemistry). My interest in it comes from its role in energy balance, particularly in synthesizing information in the hypothalamus. Since I am primarily focused on mammalian hibernation, the fact that mTOR is a serine-threonine kinase is intriguing - its known that transcription and protein translation are shut down during mammalian torpor bouts so the control mechanisms are likely to involve post-translational protein modifications such as phosphorylation. Perhaps mTOR is involved in these mechanisms.

5-body woes

I've been working for the last few weeks with Anders Jensen, Eduardo Leandro, Gareth Roberts, John Little, Manuele Santoprete, and Alain Albouy on some celestial mechanics problems. While I was in Goettingen, Anders and I tried hard to get some results on central configurations in the five-body problem. Unfortunately, we hit one very, very nasty special case in our finiteness proof, which has me musing over a couple of big polynomials that start out looking like this:




Ouch!

Back from CA and Goettingen

Blog's not dead yet...just took a 2 month hiatus. I started feeling guilty about not posting, which doesn't make much sense since its my own blog and it has very few regular readers - even fewer now!

Since my wife now has a much nicer camera for her work, I can bring her small one with me on trips. Its too bad I didn't have it in South Africa, but at least I had it in Goettingen last week where I could take a few pictures of the famous goose girl:

Carl Witty does Sage on the G1

"the entire compile took 20943 minutes of real time (about
14.5 days)"

This is just heroic, borderline legendary: compiling Sage on the Android G1. There is nothing to be done but read the post from sage-devel and see the picture.

I have compiled and run Sage 3.2.3 on my T-Mobile G1 cell phone, and
large portions of it actually work.

300 files had failing doctests; this means that all doctests passed in
864 files. A lot of the failing doctests are with pexpect (maxima,
gap, etc.); I don't know why these fail. When I try simple things
with gap and maxima, they do work. Many more tests fail due to
timeouts; the 300-second timeout is far too short for the G1.
(Doctesting any file with doctests takes >50 seconds; doctesting a
file with no doctests takes >4 seconds. The entire doctest run took
270724 seconds, or a little over 3 days.)

Unfortunately, it's far too slow to be useful for anything (just
starting Sage takes about a minute, if there's enough free memory; but
since Android likes to keep the memory full all the time, there never
is enough free memory, and it takes much longer to start). So I don't
plan to do anything further with the project.

Of course, the sensible way to do this is to find some nice fast
computer and set up a cross-compiler. I didn't do this the sensible
way; I actually did the build on the cell phone. And of course, the
build would stop every once in a while due to a bug, which I would
then patch around. So, adding up the 14 chunks of compilation
involved, the entire compile took 20943 minutes of real time (about
14.5 days) and 9438 minutes (about 6.5 days) of CPU time. You'll note
that the CPU time adds up to less than half of the real time; most of
the rest of the time was spent swapping. The G1 has about 100MB of
RAM; I set up a swap file on my micro-SD card, to allow the build to
proceed at all. On several files, the compiler uses more than 300MB.
While compiling those files, the CPU is typically less than 1% active;
I'm pretty sure that there were files that took more than a day to
compile. The phone was essentially unusable for smartphone activities
(web browsing, etc.) while the build was running. In fact, the whole
smartphone UI crashed and restarted on a fairly regular basis during
the build (I'm guessing it has some sort of watchdog timer and reboots
itself if it detects that some operation is taking an unreasonably
long time), but the build just continued anyway (running inside a
screen session).

The ATLAS tuning process took about 3.2 days (with almost as much CPU
time as real time; that didn't swap much). Skimming through the logs,
I see reports of numbers like 3 to 6 MFLOPs.

The build was performed inside a Debian armel testing chroot; it's
pretty nice being able to run real Debian on my cell phone.
(Everything works; I can ssh in and out, etc., although when it's on
the cell phone network, inbound connections are problematic because
it's behind a NAT.)

To make the whole project even more pointless, since the phone is
running real Debian (inside the chroot), I can probably just wait a
few weeks or months for Tim Abbott to get all the portability issues
fixed in the sagemath Debian package, and then install Sage on the
phone with apt-get.

Here's the processor:

cwitty@localhost:/tmp$ cat /proc/cpuinfo
Processor : ARMv6-compatible processor rev 2 (v6l)
BogoMIPS : 383.38
Features : swp half thumb fastmult edsp java
CPU implementer : 0x41
CPU architecture: 6TEJ
CPU variant : 0x1
CPU part : 0xb36
CPU revision : 2
Cache type : write-back
Cache clean : cp15 c7 ops
Cache lockdown : format C
Cache format : Harvard
I size : 32768
I assoc : 4
I line length : 32
I sets : 256
D size : 32768
D assoc : 4
D line length : 32
D sets : 256

Hardware : trout
Revision : 0080
Serial : 0000000000000000

Carl

Live from Cape Town

I arrived at AIMS (the African Institute for Mathematical Sciences) yesterday. Its a great place, right on the Muizenberg beach near Cape Town - quite a thrill after being in Duluth this time of year.

I have volunteered to teach a short course on bioinformatics algorithms here, using biopython and Sage as the computational platform. It will be very interesting to see how it goes over. I am using the Plasmodium species which cause malaria as a source of examples and projects.

Below is a satellite picture of the cape peninsula and a view of Muizenberg that includes the main AIMS building.

Integral Apollonian Packings with Sage

At the national math meetings this year I heard about some really interesting and fun work on integral Apollonian circle packings. The AMS has a nice introductory article about them. I couldn't resist trying to compute and draw some in Sage. Carl Witty greatly improved the speed of my first attempt, so what follows can be considered joint work of ours. (Sage can compute nicer PDF output of these, but blogger doesn't embed PDFs.)

def kfun(k1,k2,k3,k4):
    """
    The Descartes formula for the curvature of an inverted tangent circle.
    """
    return 2*k1+2*k2+2*k3-k4

def circfun(c1,c2,c3,c4):
    """
    Computes the inversion of circle 4 in the first three circles.
    """
    newk = kfun(c1[3],c2[3],c3[3],c4[3])
    newx = (2*c1[0]*c1[3]+2*c2[0]*c2[3]+2*c3[0]*c3[3]-c4[0]*c4[3])/newk
    newy = (2*c1[1]*c1[3]+2*c2[1]*c2[3]+2*c3[1]*c3[3]-c4[1]*c4[3])/newk
    if newk > 0:
        newr = 1/newk
    elif newk < 0:
        newr = -1/newk
    else:
        newr = Infinity
    return [newx, newy, newr, newk]

def mcircle(circdata, label = False, thick = 1/10):
    """
    Draws a circle from the data.  label = True
    """
    if label==True and circdata[3] > 0 and circdata[2] > 1/2000:
        lab = text(str(circdata[3]),(circdata[0],circdata[1]), fontsize = \
500*(circdata[2])^(.95), vertical_alignment = 'center', horizontal_alignment \
= 'center', rgbcolor = (0,0,0))
    else:
        lab = Graphics()
    circ = circle((circdata[0],circdata[1]), circdata[2], rgbcolor = (0,0,0), \
thickness = thick)
    return circ+lab

def add_circs(c1, c2, c3, c4, cutoff = 300):
    """
    Find the inversion of c4 through c1,c2,c3.  Add the result to circlist,
    then (if the result is big enough) recurse.
    """
    newcirc = circfun(c1, c2, c3, c4)
    if newcirc[3] < cutoff:
        circlist.append(newcirc)
        add_circs(newcirc, c1, c2, c3)
        add_circs(newcirc, c2, c3, c1)
        add_circs(newcirc, c3, c1, c2)

zst1 = [0,0,1/2,-2]
zst2 = [1/6,0,1/3,3]
zst3 = [-1/3,0,1/6,6]
zst4 = [-3/14,2/7,1/7,7]

circlist = [zst1,zst2,zst3,zst4]
add_circs(zst1,zst2,zst3,zst4)
add_circs(zst2,zst3,zst4,zst1)
add_circs(zst3,zst4,zst1,zst2)
add_circs(zst4,zst1,zst2,zst3)

sum([mcircle(q, label = True, thick = 1/2) for q in \
circlist]).save('./Apollonian3.png',axes = False, figsize = [12,12], xmin = \
-1/2, xmax = 1/2, ymin = -1/2, ymax = 1/2)

Protein of the Day #16: Maltase (plus a beer recipe)

I just bottled a batch of my Chocolate Cake Stout, which is:

• 1 lb of Simpon's roasted barley
  
• 1 lb of crisp amber malt
  
• 6 lbs gold malt syrup (from Northern Brewer)
  
• 1 oz Yakima Magnum hops (13.5 % Alpha acid)
  
• Safale S-04 yeast
  
• 8 oz Dutch process cocoa (from Penzey's Spices)
  
• 1 lb lactose sugar
  
• 1 whole vanilla bean (also from Penzey's).
  

Good stuff.





Maltase (alpha-D-glucosidase) is a crucial enzyme in beer making, and its regulation in response to other sugars is important to understand if you really want to grok brewing. Maltose is a disaccharide of two units of glucose; in most organisms it needs to be broken down to glucose before being used in other biochemical processes. The presence of glucose inhibits the production of maltase and maltose transporter proteins, so the glucose in a wort has to be mostly used up before the yeast will switch to consuming the maltose.

Sage at the joint math meetings

Live from DC, we're halfway throught the joint mathematics meetings. This is the second year that Sage has had a booth in the exhibit hall.

Our location is not as good as last year's, but we are still getting a good amount of foot traffic - enough to occupy most of the people here most of the time. David Harvey, David Joyner, Robert Miller and I have been manning it most of time. Jason Grout helped out this afternoon quite a bit. I may be forgetting some folks because I'm a little frazzled.

The word of mouth about Sage is increasing, many people stopping by have tried it or at least heard about it. I think its very encouraging for the future. Several people expressed interest in how to become developers.

We had an MAA panel session today on open-source software in the undergraduate curriculum. Four speakers, two of which (David Joyner and Robert Miller) talked about Sage (others on R and WeBWork).

Overall, so far the booth has been another success in raising awareness and enthusiasm for Sage. Talking to different people has made me enthused about all sorts of development projects, enough to keep me busy for at least the next year...