Twenty Four Cell, take 2

Hmm...blogger re-encodes my video and for some reason their version looks like crap, so I won't even leave it up. I think my new attempt has much better lighting, and the faces have translucent panes now. But here is a still shot:



Three sizes of the new version:
small (320x200)
medium (640x400)
large (1280x800).

Witch of Maria Agnesi

There's one on wikipedia like this, but for an upcoming class I wanted to do it in Sage:




xtreme = 4.1
myaxes = line([[-xtreme,0],[xtreme,0]],rgbcolor = (0,0,0))
myaxes = myaxes + line([[0,-1],[0,2.1]],rgbcolor = (0,0,0))
a = 1.0
t = var('t')
npi = RDF(pi)
def agnesi(theta):
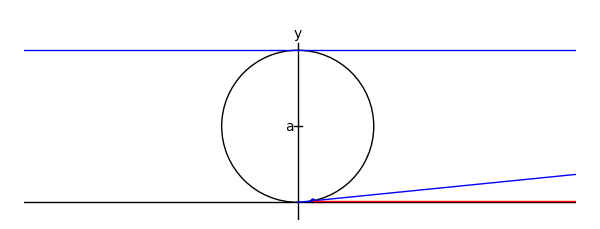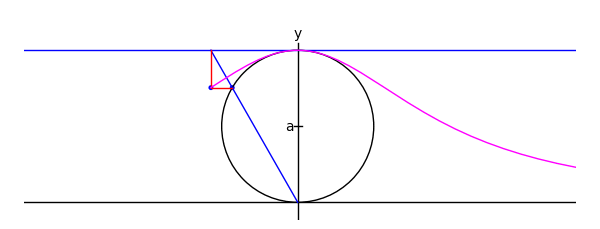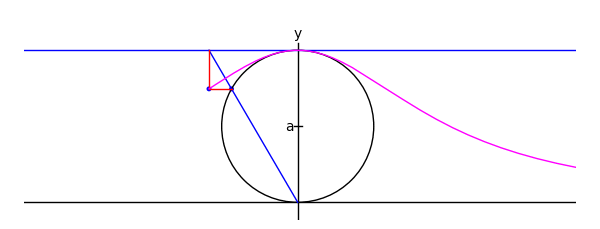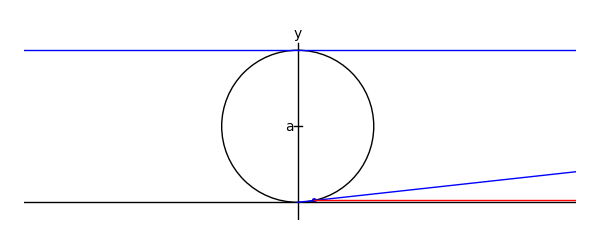
mac = circle((0,a),a,rgbcolor = (0,0,0))
maL = line([[-xtreme,2*a],[xtreme,2*a]])
maL2 = line([[0,0],[2*a*cot(theta),2*a]])
p1 = [2*a*cot(theta),2*a*sin(theta)^2]
p2 = [2*a*cot(theta)-cot(theta)*(2*a-2*a*sin(theta)^2),2*a*sin(theta)^2]
maL3 = line([p2,p1,[2*a*cot(theta),2*a]], rgbcolor = (1,0,0))
map1 = point(p1)
map2 = point(p2)
am = line([[-.05,a],[.05,a]], rgbcolor = (0,0,0))
at = text('a',[-.1,a], rgbcolor = (0,0,0))
yt = text('y',[0,2.2], rgbcolor = (0,0,0))
xt = text('x',[xtreme + .1,-.1], rgbcolor = (0,0,0))
#tt = text('t',[.15,.1], rgbcolor = (0,0,0))
matext = at+yt+xt
ma = mac+myaxes+maL+am+matext+maL2+map1+maL3+map2
return ma

def witchy(theta):
ma = agnesi(theta)
agplot = parametric_plot([2*a*cot(t),2*a*sin(t)^2],[t,.001,theta], rgbcolor = (1,0,1))
return ma+agplot

a2 = animate([witchy(i) for i in srange(.1,npi-.1,npi/60)]+[witchy(i) for i in srange(npi-.1,.1,-npi/60)], xmin = -3, xmax = 3, ymin = 0, ymax = 2.3, figsize = [6,2.3], axes = False)

a2.show()


24 cell movie

This is basically a test of my workflow for a more ambitious project, but its somewhat amusing in its own right. The original 48 MB version is here (much better quality).

Michael Corral's Calculus 3 book

Last year I became aware of the fantastic free calc 3 book by Michael Corral. His website for it is here. I wanted to be able to compile the latex source files myself but couldn't get it to work on my mac or windows machines. I just gave it another try and finally succeeded on OS X.

Besides using his calc3book.sh script, I found it necessary to:

1) install pgf/tigz.
2) put picins.sty in my tex directory
3) Put the metapost files from m3Dplain in my tex directory.

Its a beautifully done book, so I am excited to learn some of the tricks Corral uses.

Hearing a trigonometric identity

If you force a harmonic oscillator with natural frequency w_0 with a sinusoidal force of frequency w, the resulting steady-state is a linear combination of those two frequencies. If its something in the audible range, you hear either the two seperate frequencies or one frequency with a beat if they are close together. In other words, you hear either the right or left hand side of the identity shown below.



Sage source code available here. Ironically, because of my use of html I can't seem to show the source directly here.

Small frequency difference.

Smallish frequency difference (close to the Ma Bell tone).

Intermediate frequency difference.

Large frequency difference - you definitely hear it as a 2-note chord.